Kepler’s Law in Hindi

Kepler’s Law in Hindi

Kepler’s Law in Hindi (केप्लर का नियम हिंदी में) आइये दोस्तों आज हम केप्लर के गति के नियम हिंदी में पड़ेंगे जोकि satellite communication से जुड़े हुए है। 

ग्रहों की गति के केप्लर के नियम (Kepler’s Laws of planetary motion)

केप्लर के नियम (Kepler’s laws) अंतरिक्ष में किन्हीं दो पिंडों पर सामान्य रूप से लागू होते हैं जो गुरुत्वाकर्षण के माध्यम से आपस में interact करते हैं। दो निकायों (two bodies) में से अधिक विशाल या बड़ी को प्राथमिक (primary), दूसरे, द्वितीयक (secondary) या उपग्रह (satellite) के रूप में संदर्भित किया जाता है।

केप्लर के नियम: जोहान्स केप्लर (Johannes Kepler) ने अपने जीवनकाल के अध्ययन के आधार पर ग्रहों की गति की व्याख्या करने वाले तीन अनुभवजन्य अभिव्यक्तियों (three empirical expressions) का एक सेट दिया। इन नियमों की बाद में पुष्टि हुई जब न्यूटन ने गुरुत्वाकर्षण का नियम दिया। हालांकि ग्रहों की गति के लिए दिए गए ये नियम पृथ्वी के चारों ओर प्राकृतिक और कृत्रिम उपग्रहों की गति के लिए या किसी अन्य पिंड के चारों ओर घूमने वाले किसी भी धूमने वाली वास्तु के लिए समान रूप से मान्य हैं। यहां, इन कानूनों या नियमों पर पृथ्वी के चारों ओर कृत्रिम उपग्रहों की गति के संदर्भ में चर्चा की जाएगी।

मुख्य: रूप से Kepler’s Law in Hindi (केप्लर का नियम हिंदी में) तीन तरह के है, तो चलिए पड़ते है-

केप्लर का पहला नियम (Kepler’s First Law)

केप्लर का पहला नियम: पृथ्वी के चारों ओर एक उपग्रह की कक्षा अण्डाकार होती है और पृथ्वी का केंद्र दीर्घवृत्त (ellipse) के किसी एक केंद्र पर स्थित होता है। अण्डाकार कक्षा की विशेषता इसकी अर्ध-प्रमुख धुरी a और विलक्षणता e है। उत्केंद्रता (Eccentricity) दीर्घवृत्त के केंद्र और उसके दोनों फोकी (foci)  (= ae) के बीच दीर्घवृत्त के अर्ध-प्रमुख अक्ष के बीच की दूरी का अनुपात है।

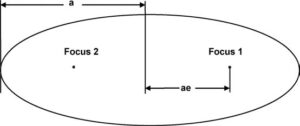
एक गोलाकार कक्षा एक अंडाकार कक्षा का एक विशेष प्रकार होता है, जहां foci एक केंद्रीय बिंदु देने के लिए एक साथ विलीन हो जाती है और विलक्षणता (eccentricity) शून्य हो जाती है। एक अण्डाकार उपग्रह कक्षा के अन्य महत्वपूर्ण मापदंडों में इसकी apogee (पृथ्वी के केंद्र से कक्षा का सबसे दूर का बिंदु) और perigee (पृथ्वी के केंद्र से कक्षा का निकटतम बिंदु) दूरियां शामिल हैं। किसी भी अण्डाकार गति के लिए, ऊर्जा संरक्षण का नियम कक्षा के सभी बिंदुओं पर मान्य होता है।

ऊर्जा के संरक्षण का नियम कहता है कि ऊर्जा को न तो बनाया जा सकता है और न ही नष्ट किया जा सकता है; इसे केवल एक रूप से दूसरे रूप में परिवर्तित किया जा सकता है। उपग्रहों के संदर्भ में, इसका अर्थ है कि किसी उपग्रह की गतिज और स्थितिज ऊर्जा का योग हमेशा स्थिर रहता है।

केप्लर का दूसरा नियम (Kepler’s Second Law)

उपग्रह और पृथ्वी के केंद्र को मिलाने वाली रेखा समान समय अंतराल में कक्षा के तल में समान क्षेत्रों को पार करती है; यानी वह दर (dA/dt) जिस पर यह क्षेत्र A को पार करता है, स्थिर है।

swept-out area के परिवर्तन की दर निम्न द्वारा निकली जाती है,

\frac{dA}{dt}=\frac{angular momentum of the satellite}{2m}

जहाँ m उपग्रह का द्रव्यमान है। इसलिए, केप्लर का दूसरा नियम भी संवेग के संरक्षण के नियम के बराबर है, जिसका अर्थ है कि त्रिज्या वेक्टर (radius vector) और रेखीय संवेग (linear momentum) के घटक का गुणनफल, त्रिज्या वेक्टर के लंबवत होता है तथा यह कक्षा (orbit) के सभी बिंदुओं पर स्थिर होता हैं। 

m द्रव्यमान के उपग्रह का कोणीय संवेग mr2ω द्वारा दिया जाता है, जहाँ ω उपग्रह का कोणीय वेग है। 

केप्लर का तीसरा नियम (Kepler’s Third Law)

केप्लर के तीसरे नियम के अनुसार, जिसे अवधियों के नियम (law of periods) के रूप में भी जाना जाता है, किसी भी उपग्रह की समयावधि का वर्ग उसकी अण्डाकार कक्षा के अर्ध-प्रमुख अक्ष के घन के समानुपाती होता है।

समय अवधि के लिए अभिव्यक्ति निम्नानुसार प्राप्त की जा सकती है। त्रिज्या r के साथ एक गोलाकार कक्षा ग्रहण की जाती है। याद रखें कि एक वृत्ताकार कक्षा एक अण्डाकार कक्षा का केवल एक विशेष मामला (special case) है, जिसमें अर्ध-प्रमुख अक्ष और अर्ध-लघु अक्ष दोनों त्रिज्या के बराबर हैं। केन्द्रापसारक बल (centrifugal force) के साथ गुरुत्वाकर्षण बल (gravitational force) की बराबरी करने पर मिलता है

\frac{Gm_{1}m_{2}}{r^{2}}=\frac{m_{2}\nu ^{2}}{r}

उपरोक्त समीकरण में v को r से बदलने पर प्राप्त होता है

\frac{Gm_{1}m_{2}}{r^{2}}=\frac{m_{2}\omega^{2}r^{2}}{r}=m_{2}\omega^{2}r

जो \omega^{2}=Gm_{1}/r^{3} देता है ।  ω = 2π/T

को प्रतिस्थापित करने पर

T^{2}=\left ( \frac{4\pi ^{2}}{Gm_{1}} \right )r^{3}

इसे इस प्रकार भी लिखा जा सकता है

T=\left ( \frac{2\pi}{\sqrt{\mu }} \right )r^{3/2}

उपरोक्त समीकरण अण्डाकार कक्षाओं के लिए अच्छा है बशर्ते r को अर्ध-प्रमुख अक्ष a द्वारा प्रतिस्थापित किया जाए। यह एक अण्डाकार कक्षा की समयावधि के लिए अभिव्यक्ति देता है:

T=\left ( \frac{2\pi}{\sqrt{\mu }} \right )a^{3/2}